Difference between revisions of "Lund string model"
| Line 12: | Line 12: | ||
When the yo-yo is minimally extended (at ''t = 0'' in the figure), all energy is stored in the quarks. When the string is maximally stretched, all energy is stored in the string, and the quarks turn around. | When the yo-yo is minimally extended (at ''t = 0'' in the figure), all energy is stored in the quarks. When the string is maximally stretched, all energy is stored in the string, and the quarks turn around. | ||
| + | ==String breaking== | ||
| + | The string arising from an initial, colour connected parton pair, must break into smaller pieces, in order to produce hadrons. The produced hadron carries away some lightcone momentum from the string, and the when it runs out, the breaking ends. A produced hadron carries away momentum according to the Lund symmetric fragmentation function, which is a distribution function in the momentum fraction ''z'': | ||
| + | |||
| + | <math> | ||
| + | f(z) = N\frac{(1-z)^a}{z}\exp\left(-\frac{-bm^2_\perp}{z} \right). | ||
| + | </math> | ||
| + | |||
| + | Here ''a'' and ''b'' are parameters, <math>m_\perp = \sqrt{m^2 + p^2_\perp}</math> is the transverse mass and ''N'' normalises the distribution. | ||
==References== | ==References== | ||
{{Reflist}} | {{Reflist}} | ||
Revision as of 12:04, 4 January 2017
The Lund String model[1] is a model for hadronisation, i.e. the process of transforming a partonic final state to a hadronic one.
The model is built upon a "string" analogy, a potential linearly rising with the distance between the two quarks. At some point, the potential energy stored in the string is so large, that the string will break into hadrons. The Lund model includes the possibility for creation of hadrons with light quark content (u, d and s-type), mesons as well as baryons.
The Lund string hadronisation is implemented in the Pythia event generator, and can be interfaced stand-alone.
The yo-yo model for mesons
The Lund string model is built up around a string model for mesons, where mesons are described as two massless quarks moving in 1+1 dimensions, connected by a massless string, making the quarks turn around when the string is maximally extended. This type of movement pattern (called directrix) is called the yo-yo because of its resemblance to the toy. (See ref. [2] for a through discussion of several directrices)
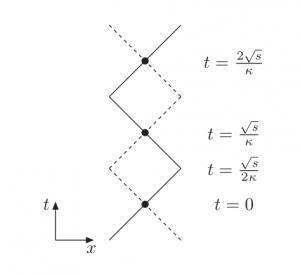
When the yo-yo is minimally extended (at t = 0 in the figure), all energy is stored in the quarks. When the string is maximally stretched, all energy is stored in the string, and the quarks turn around.
String breaking
The string arising from an initial, colour connected parton pair, must break into smaller pieces, in order to produce hadrons. The produced hadron carries away some lightcone momentum from the string, and the when it runs out, the breaking ends. A produced hadron carries away momentum according to the Lund symmetric fragmentation function, which is a distribution function in the momentum fraction z:
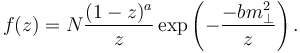
Here a and b are parameters,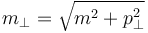 
is the transverse mass and N normalises the distribution.
References
Template:Reflist- ↑ B. Andersson, “The Lund model,” Camb. Monogr. Part. Phys. Nucl. Phys. Cosmol. 7 (1997) 1–471
- ↑ X. Artru, “Classical String Phenomenology. 1. How Strings Work,” Phys. Rept. 97 (1983) 147.
- ↑ C. Bierlich, “Rope Hadronization, Geometry and Particle Production in pp and pA Collisions“ PhD thesis, Lund University, 2017 Full text
