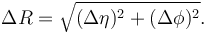Difference between revisions of "Angular distance"
From Particle Wiki
| Line 7: | Line 7: | ||
:<math>\Delta R = \sqrt{(\Delta\eta)^2 + (\Delta\phi)^2}.</math> | :<math>\Delta R = \sqrt{(\Delta\eta)^2 + (\Delta\phi)^2}.</math> | ||
| + | <math>x=5</math> | ||
== At lepton colliders == | == At lepton colliders == | ||
At [[Lepton collider|lepton colliders]], the vector angle between the object momenta may be used directly. | At [[Lepton collider|lepton colliders]], the vector angle between the object momenta may be used directly. | ||
Revision as of 17:18, 17 July 2017
The angular distance (or angular separation) between two objects tells how much two objects are moving in the same direction. It is usually denoted ΔR (delta R).
At hadron colliders
At hadron colliders, the angular distance is usually defined in a way that is invariant under longitudinal boosts. This is achieved by using the pseudorapidity difference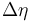 
of the objects rather than an actual angle. In the transverse plane, the momentum of the initial state is (essentially) zero, so the azimuthal angle difference 
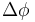can be used directly. This gives the definition:
At lepton colliders
At lepton colliders, the vector angle between the object momenta may be used directly.
