Sphericity

The sphericity tensor is the basis for calculation of Event Shape observables, a series of observables particularly suited for 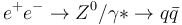$e^+ e^- \rightarrow Z^0/\gamma* \rightarrow q\bar{q}$, and routinely used in several LEP analyses.

Definition

The sphericity tensor is defined as:

$S^{ab} = \frac{\sum_i p_i^a p_i^b}{\sum_i |p_i|^2}.$

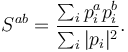
Here 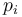$p_i$ are the four-momenta of all particles in an event. Superscript a and b indicates spatial components, and the sphericity tensor can thus be represented as a 3-by-3 matrix. As such, three eigenvalues can be found. If they are ordered as 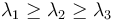$\lambda_1 \geq \lambda_2 \geq \lambda_3$, the sphericity is defined as:

$S = \frac{3}{2}(\lambda_2 + \lambda_3).$

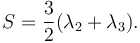
The similar quantity aplanarity is defined as:

$A = \frac{3}{2}\lambda_1$

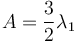
Physical meaning

The eigenvector corresponding to 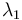$\lambda_1$ is called the sphericity axis. S measures the amount of 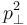$p_\perp^2$ with respect to that axis, and is constrained to values 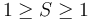$1 \geq S \geq 1$. An event with sphericity 0 is a clean dijet event, and sphericity 1 signifies an isotropic event.

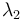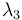The eigenvectors corresponding to $\lambda_2$ and $\lambda_3$ spans a plane, the so-called sphericity plane. Aplanarity measures the 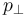$p_\perp$ out of that plane, is constrained to 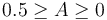$0.5 \geq A \geq 0$. Similarly to S, A is used to signify the isotropicity of the event.

Data and description

Sphericity and aplanarity was measured in all the LEP experiments, and the data are particularly important for tuning of parton showers. Measurements and comparisons to event generators can be found at MCplots for sphericity and aplanarity.

The 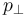$p_\perp$ out of the sphericity plane is a particularly interesting observable, as it has been problematic to describe for all the standard parton shower generators, see e.g. the measurement by ALEPH:

File:Http://mcplots.cern.ch/cache/plots/zhad-pToutSph-General-Purpose MCs.Defaults-aleph1-charged-ee-91-.png

ss

<image></image>