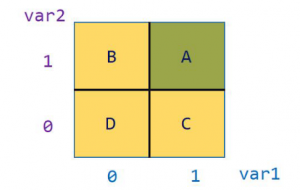
ABCD method
The ABCD method is commonly used to estimate the size of a background contribution from real data (as opposed to Monte Carlo simulation). It takes its name from the fact that it uses four regions, which are sometimes labelled A, B, C, D. One of the regions is the signal region for which one wishes to make the background estimate. The other three are obtained by reverting two different signal selection criteria X and Y:
Region A: pass X and pass Y (this is the signal region) Region B: fail X and pass Y Region C: pass X and fail Y Region D: fail X and fail Y
It is essential that the criteria X and Y can be treated as uncorrelated. This is true if the probability to pass criterion X does not (significantly) depend on whether criterion Y passes, and vice versa. With this assumption, the following relation holds for the numbers of background events in the four regions:
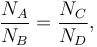
or, equivalently,
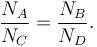
This means that the event yield in the signal region A due to the background process can be predicted by measuring the event yields due to this background in control regions B, C, D:
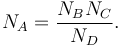
Contributions other than the background of interest must be subtracted in the regions B, C, D. This can often be done using MC simulation. The method is usually most robust if the criteria X and Y can be chosen in such a way that the regions B, C, D are very much dominated by the background of interest. In particular, there should only be very little predicted signal leakage into those regions.
Correlations between selection criteria
The method can be extended to work in situations where correlations between the selection criteria X and Y cannot quite be neglected. In that case, a correlation factor 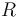 can be included, so that the equation governing the ratios of event counts becomes
can be included, so that the equation governing the ratios of event counts becomes
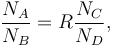
The ratio 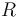 can be determined using MC simulation.
can be determined using MC simulation.