Missing energy
Missing energy, often denoted 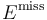 , refers to energy that is not detected in a detector but is expected because of conservation of momentum. It is also called missing momentum. Both terms are used to refer both to the vectorial form
, refers to energy that is not detected in a detector but is expected because of conservation of momentum. It is also called missing momentum. Both terms are used to refer both to the vectorial form 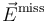 and its norm
and its norm 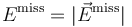 .
.
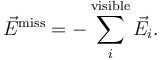
Based on conservation of momentum, the missing energy in an event is equal in size and opposite in direction to the visible energy in the event:
Missing energy occurs when particles that do not interact with the detector sufficiently to be detected are produced in the collisions, such as neutrinos and possibly unknown new particles, but it can also be due to mismeasurement of detectable particles.
In hadron colliders, the longitudinal momentum component of the initial state is unknown, because hadrons are composite particles whose energy is shared by their constituent partons and constantly transferred between them. Therefore, conservation of momentum can only be applied to infer missing energy in the transverse plane, this is called missing transverse energy or missing transverse momentum, 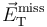 .
.
In collider detectors, missing (transverse) energy is the detector signature of neutrinos as well as hypothetical new particles that do not interact with the detector, such as the lightest supersymmetric particle.