Energy resolution (ATLAS)
This article only describes the situation for electrons and photons and could be expanded.
For electrons and photons in ATLAS, the relative energy resolution 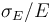 of the electromagnetic calorimeter can be parametrised as
of the electromagnetic calorimeter can be parametrised as
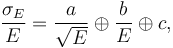
where the sampling-term coefficient 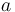 , the noise-term coefficient
, the noise-term coefficient 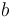 and the constant-term
and the constant-term 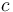 are pseudorapidity-dependent parameters. The sampling term contributes mostly at low and intermediate energy and depends on calorimeter shower and sampling fluctuations. The noise term is dominated by the pileup noise in the standard LHC data taking (i.e. at an average number of interactions per bunch crossing of the order of a few dozen). At higher energies, the relative energy resolution tends asymptotically to the constant term,
are pseudorapidity-dependent parameters. The sampling term contributes mostly at low and intermediate energy and depends on calorimeter shower and sampling fluctuations. The noise term is dominated by the pileup noise in the standard LHC data taking (i.e. at an average number of interactions per bunch crossing of the order of a few dozen). At higher energies, the relative energy resolution tends asymptotically to the constant term, 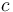 , which in ATLAS has a design value of 0.7%. For electrons and converted photons, interactions with the material in front of the calorimeter also contribute to the
, which in ATLAS has a design value of 0.7%. For electrons and converted photons, interactions with the material in front of the calorimeter also contribute to the 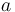 and
and 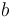 terms.
terms.
A relative uncertainty of 10% on the sampling coefficient 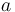 is assumed based on test-beam data. The constant term
is assumed based on test-beam data. The constant term 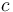 is extracted from
is extracted from 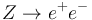 measurements. In standard LHC data taking conditions, the energy resolution at low energy is dominated by the noise coefficient
measurements. In standard LHC data taking conditions, the energy resolution at low energy is dominated by the noise coefficient 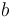 and measuring the sampling coefficient
and measuring the sampling coefficient 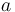 to reduce its uncertainty is difficult.
to reduce its uncertainty is difficult.